报告题目：The scattering of fractional Schrödinger operators with short range potentials
报 告 人： 黄天骁（中山大学 副教授）
会议时间：2021/9/13 上午11:30开始
会议地点：腾讯会议线上报告
会议链接：//meeting.tencent.com/dm/6grYEHHMPJei?rs=25
会议 ID：106 472 397
报告摘要: I will first review some basic concepts and classical results in the short range scattering theory for the Schrödinger operator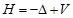 
, along with a brief introduction of the short range perturbation theory for simply characteristic operators including the higher order Schrödinger operators 
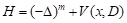typically. Then I will explain how to establish the short range scattering theory for the fractional Schrödinger operator 
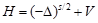in the full range 
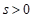. When 
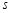is not even, the challenge comes from the non-local aspect of 
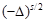, and the crucial study of its limiting absorption principle is related to a sharp Fourier restriction property. I will also give explicit examples on the non-existence of wave operators, to show that our short range condition is sharp with respect to the decay assumption on 
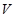, where the decay threshold is new. This is a joint-work with Rui Zhang and Quan Zheng.
个人简介: 黄天骁本科与博士毕业于华中科技大学博彩导航
，现为中山大学数学学院（珠海）副研究员，研究方向为调和分析及其在高阶和分数阶色散方程中的应用，主要工作发表于JFA, JDE, CPDE等国际一流期刊。其在高阶薛定谔算子相关的函数空间估计，一致预解式估计，唯一延拓性，散射理论等取得了系列成果，得到国际同行的广泛引用与好评。
