报告题目：Stability of Sobolev Inequality
报 告 人：Juncheng Wei（加拿大英属哥伦比亚大学 教授）
会议时间：2021/9/16 上午10:00开始
会议地点：腾讯会议线上报告
会议链接//meeting.tencent.com/dm/AS4GlQEVu98R
会议 ID：287 959 944
报告摘要：In this talk, I will discuss the stability of Sobolev inequality from the view of critical point, i.e. Struwe's decomposition. Suppose that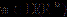 
. In a seminal work, Struwe proved that if 
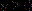and 
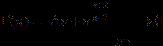, then 
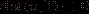, where 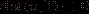denotes the 
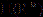-distance of u from the manifold of sums of Talenti bubbles. Ciraolo, Figalli and Maggi (2018) obtained the first quantitative version of Struwe's decomposition with one bubble in all dimensions, namely 
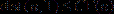. For Struwe's decomposition with two or more bubbles, Figalli and Glaudo (2020) showed a striking dimensional dependent quantitative estimate, namely 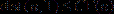when
, while this is false for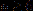 
. In this talk, I will present the following optimal estimate
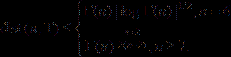. Finally connection with isoperimeter inequalities and other geometric/Sobolev inequalities will also be discussed.
报告人简介：魏军城教授，著名华人数学家，现任加拿大英属哥伦比亚大学国家讲座教授、香港中文大学伟伦讲座教授, 加拿大皇家科学院院士。 1989年获武汉大学学士学位，之后经国家陈省身奖学金项目选派到美国攻读博士学位，1994年获Minnesota(明尼苏达)大学博士学位。现为加拿大英属哥伦比亚大学国家讲座教授(Canada Research Chair)和香港中文大学伟伦(Wei Lun)讲座教授。魏军城教授的主要研究领域是非线性偏微分方程、凝聚现象与爆破、数学生物学。 他于2010年获华人数学家大会晨兴银奖、2010年获教育部自然科学一等奖、2014年应邀在第27届国际数学家大会上做45分钟报告、2014年入选教育部讲座教授、2020年获得加拿大数学会Jeffery-Williams Award。魏军城教授在非线性偏微分方程和生物数学等领域取得了国际公认的成就，完整解决了著名的De Giorgi猜想，并在几何流的爆破解构造上取得了享誉国际的成果。其相关论文发表在Ann. of Math., Invention等国际顶级期刊。其研究成果被引次数超过一万多次，其系列开创性的工作给许多重大公开问题带来崭新的方法，具有前瞻性和划时代的意义。
