报告题目:Convergence rates in homogenization of parabolic systems with locally periodic coefficients
报 告 人:徐侥(中国科学院数学与系统科学研究院数学所 博士后)
报告时间:2020年7月9日(星期四)下午2点半开始
报告地点:腾讯会议线上报告
会议链接://meeting.tencent.com/s/RCXnGyfRBFnV
会议 ID:469 636 475
报告摘要:This talk mainly concerns with the quantitative homogenization of second-order parabolic systems with time-dependent locally periodic coefficients in  cylinders, i.e.,
cylinders, i.e.,
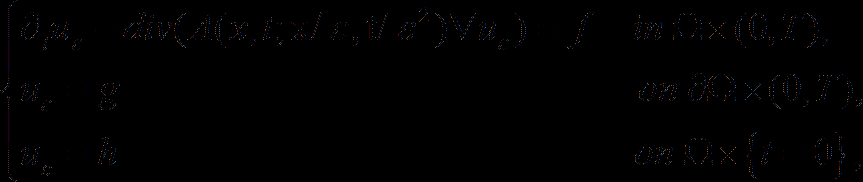
where  is a bounded
is a bounded  domain in
domain in  , the matrix
, the matrix 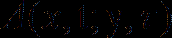 defined on
defined on 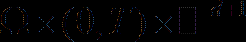 is bounded, elliptic and 1-periodic in
is bounded, elliptic and 1-periodic in 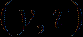 , and
, and 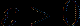 is a parameter. Under nearly minimum smoothness assumptions on
is a parameter. Under nearly minimum smoothness assumptions on 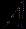 which indicate the
which indicate the  order differentiability in
order differentiability in  and
and 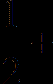 order differentiability in
order differentiability in  , the sharp-order scale-invariant convergence rate to some
, the sharp-order scale-invariant convergence rate to some 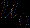 is established. To do this, we employ fractional derivatives on intervals to build several almost optimal estimates for the macroscopic smoothing operator, and derive a new estimate for the integrals on temporal boundary layers. This extends the previous work [Y. Xu and W. Niu, Comm. Partial Differential Equations, 2020] about elliptic systems with stratified structure.
is established. To do this, we employ fractional derivatives on intervals to build several almost optimal estimates for the macroscopic smoothing operator, and derive a new estimate for the integrals on temporal boundary layers. This extends the previous work [Y. Xu and W. Niu, Comm. Partial Differential Equations, 2020] about elliptic systems with stratified structure.
报告人简介:徐侥,中国科学院数学与系统科学研究院数学研究所博士后。2012年本科毕业于南京大学数学系,并于2019年在南京大学获得理学博士学位,博士期间曾在美国肯塔基大学联合培养两年。现主要从事于偏微分方程均匀化理论的研究工作,系列工作发表在 JFA、CPDE、JDE、AMPA、Asymptot. Anal.、DCDS等国际重要期刊上。











